这是关于量纲分析物理基础系列文章的第二篇,这个系列由如下几篇文章组成:
量纲分析物理基础:简介
量纲分析物理基础:物理量和方程(本文)
量纲分析物理基础:量纲分析
量纲分析物理基础:物理量数字值固定的量纲分析
2.1物理性质(physical properties)
科学始于对事物和事件的观察和精确描述。我们面对面地讨论支持量纲分析的基础是我们理解量纲分析的第一步:用绝对概念来描述是不可能。我们只能将一个事物与另一个事物进行比较,从而“抓住事物的本质。”当我们说某物“是”一棵树时,其实简单地来说,是指它有的特征与我们称为“树”的事物很相似。
我们的大脑已进化到一见到后就立即能识别出树来,但真正要描述像树一样的事物却是很复杂的一件事。物理学开始将描述过程分成简单的小过程来描述事物。物事或事件可以通过诸如长度、质量、颜色、形状、速度和时间等属性(property)来描述。这些属性都不可能有绝对的定义,它们只表示与其它某些事物的相似性:我们说,物体可以用米尺似的长度,有橘子似的黄色、与一大块材料相似的重量,或者有球体一样的开关。对相似性的参考可以做得更精确,但本质上,描述就是一个物体与其它我们所知物体之间相似性的比较,除了比较,我们不能做得更多了。
通过定义并标准化比较操作,可以确定两个样品之间是相等(A=B)还是不等(A≠B)(当谈论真实的物理特性而非数字值时,我们要用粗体字)。这个操作,就是一个完整的物理程序,它定义了物理属性,这是物理学体验到的第一个属性。同种属性(简单地说就是同一属性)可以通过同一比较操作来进行比较。不同种类的属性不能比较,因为它们之间不存在比较等同性的操作。问特定的质量在物理上是否等于特定的长度这样的问题是毫无意义的:没有一种程序可以做这样的比较。
如果只用比较操作定义物理属性,那么就能用一个程序来确定两个样品是相等还是不相等,但还有一些概念不能两者之间那一个大那一个小,形状和颜色就是一个实例。我们有程序可以确定两个物体之间有相同的形状和颜色,但当问到正方形是否比圆形更大还是更小时或者问到绿色比白色更大还是更小时,就没有意义了。形状和颜色这一类的特性属性非常有用,但在数量分析中,要处理相对数量时,它就无用武之地了。
2.2物理量和基本物理量
科学始于对世界的观察和描述,便它的终极目的是从这些观察推断出最简单和普遍的(也即节约的)、描述物理世界的规律。数学语言描述作为描述这些规律的理想工具不是偶然的,它满足我们对某些物理属性的约束要求,使我们能对这些物理属性做定量分析。能做定量分析的物理属性我们称为“物理量”。
有两种类型的物理量:基本物理量和导出物理量。基本物理量,按物理规律定义,形成一个完整的集合,组成了一个开放系统,可以导出其它必要的物理量。基本物理量和导出物理量一起形成了对物理世界做定量分析的基础。
基本物理量由特定的两个物理操作所定义:
- 比较操作定义物理属性的两个样品值A和B是否相等(A=B)或者是不相等(A≠B);
- 加操作定义物理属性两个样品值相加结果(C=A+B)的含义。
具有相同比较操作和加操作的基本物理量是相同的物理量(也即是同一物理量的不同样品值)。由于物理量被加各到一起,所以加操作A+B定义了同种物理量C。不具有相同的比较和加操作的物理量不能进行比较操作和加操作,因为没有一种程序可以进行这样的操作。所有的物理量都是物理事物或事件的属性。它们本身不是物理事物或事件。比较操作和加操作涉及到在分析时对事物或事件的物理操作过程。
比较操作和加操作是物理性的,但它们应该有一定的特性使得它们能模仿相应的数学上对纯粹数字上的比较操作和加操作:
- 比较操作必须遵守传递律(如果A=B并且B=C,那么A=C);
- 加操作必须遵守交换律(A+B=B+A)和联合律[A+(B+C)=(A+B)+C]
两个操作共同定义了以下的物理概念:
- 大小的概念(如果正在一个有限的B,并且A+B=C,那么C>A);
- 减法的概念(如果A+B=C,那么A≡C-B);
- 同纯粹数字相乘(如果B=A+A+A,那么B≡3A)以及
- 同纯粹数字相除(如果A=B+B+B,那么B≡A/3)。
因此基本物理量是一种满足数学操作的物理量:它能作比较和加法操作,也能作与纯粹数字的乘法和除法操作。这些操作都是在同种类的物理上实施的,并且最终获得的物理量也是同一种类的,每一个操作都要遵守在纯粹数字上的相应操作规则。
这样不仅能抓住事物的本质,还能用数学语言来表述事物的本质。值得注意的是,上述数学操作中任何一种操作都没有定义物理量,这一点特别重要。比如,没有一种操作会可以明确地表述质量乘以时间的概念,或者表述质量与长度的乘积(这个我们以后还会提到)是一种什么样的概念;我们也不能指出某些明确的物理事物“就是”长度的立方要或“就是”时间的自然对数。乘积、比例、幂、指数以及其它诸如三角函数和对数函数都是为纯粹数字定义的,它们都不涉及到相应的物理的操作。
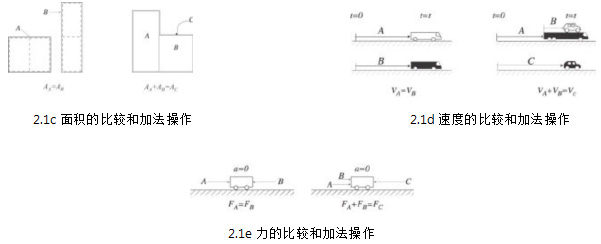
图2.1例示了在某些已知物理量上的比较操作和加法操作,这些物理量都可以选择为基本物理量。图例以一种简单的卡通式的方式显示了对这些物理量的操作,当然,我们知道每一个操作都是同仔细设计的程序真实相关的,并且有关这些程序的这一整套概念还会是相当复杂的。我们这样认识世界,非常像Dr.Samuel Johnson对世界的认识一样,当被问到他是如何知道真实物理世界是存时,他只是用脚跺跺地面,因为这些都是理所当然的。
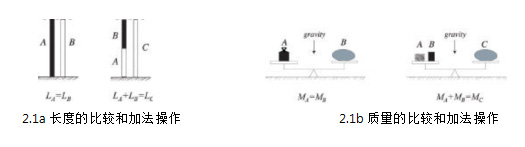
长度和质量的比较操作是相似的,这里要着重提出来的问题是:质量指的是“引力质量”。如果第三个质量在同一个相对位置分别与两个质量的引力相同,那么这两个质量是相等的,这样定义的质量称为引力质量。
在图2中未提到时间,极大的原因在于为时间所定义操作不遵守简单性原则。时间的概念更深地植根于生物体,它毕竟是我们对事件过程的体验,它是从事件一发生就开始的持续。时间是对事件的特征化而非对事物的特征化。亚里士多德认为时间是运行量纲,他是我们喜欢的一位诗人,但科学家们对此却无动于衷。如果我们接受更为务实的概念,即认为时间是理想化的时钟或秒表,我们在其上所定义比较和加法操作,这样就更类同于爱因斯坦对大众讲述它的相对论了(1952)。无论这些时钟是沙漏还是原子钟,它们只是精度不同,但其内在本质却是一样的。在当前这个条件下,时间“是”什么的讨论是毫无意义的,它仅仅是我们要定义操作的问题罢了5。
力的概念最初来源于肌肉的效果,随后被正式定义为作用在物体上的合力(作用在物体上的全部力的向量和)所引起物体速度变化的观察结果。力的定向性很重要,力是一个向量物理量。
习惯于认为速率是“距离除以时间”和面积是“长度的平方”的读者,可能会奇怪带有自身的比较操作和加法操作的速率和时间也会成为(可能的)基本物理量出现在图2.1中。我们将它们包含在图2.1中主要是为了向读者展示基本物理量是与选择相关的一件是。速率(如果考虑方向即为速度)是确切的运动发生,并且我们可以定义一套可为人所接受的程序来确定两个速度是相等或不相等,如图2.1d。因此速度是可以作为基本物理量的,只要我们做这样的选择,面积也一样。注意:两个形状的不一定要在“形式上全等”才是面积相等,只要其中一个通过切割和拼装后与另一个相等即可以认为面积相等;面积的比较涉及到加法操作,加法操作也涉及到比较操作。
我们已经讨论过,尽管形状和颜色是可以为人们所接受的物理量,但它们不能成为基本物理量因为它们缺乏可接受的加法操作。形状不能成为基本物理量是很明显的:正方形加圆形是什么?但是为什么颜色也不能成为基本物理量呢?我们知道颜色可以按照定义发的规则进行加法操作,比如当红光加上绿光会得到黄光,难道这还不能成为加法的物理定义吗?答案是“No”。蓝光行于蓝光,但是按照这个操作规则,蓝光加蓝光仍然等于蓝光,加法操作结果不是唯一的:对于任何一种颜色,任意的数字n,都存在nA=A。所以颜色不是物理量(而且没有可能的单位可以用来测量颜色)。但是,固执的读者可能争辩,一个物体的颜色是由它所反射的光波波长所决定的,而光波的波长是可以相加的,难道这个也不是一种可以接受的加法规则吗?我们的回答仍然是“No”。这个规则是长度的加法规则而不是我们所感受的颜色的加法规则。
2.3单位和数字值
有了定义基本物理量的两个操作,我们就能够将任何一种物理量表示为同种物理量的标准样品值的倍数,也即用“单位来测量”。标准样品,即测量单位是可以随意选择的。比较操作允许我们复制单位,而加法操作允许我们验明和复制分数倍数单位。在物理上,测量过程就复制单位的过程,最后将单位和它的分数倍数的复制品相加就是所测量的物理量(图2.2)。单位的整数倍数和分数倍数的数量就是被测物理量的数字值。如果a是物理量A的测量单位,测量过程所得到的数字值为A,即:
A=Aa
整个测量过程是一个物理过程。唯一涉及到的数学过程就是计数,记录自制单位的整数倍数和分数倍数,一旦被测物理量和单位的整数复制品和分数复制品之各相等时,测量过程就终止。
图2.1使用单位的测量过程和数字值
需要强调的是,具体的测量数字与随意选择的方法有关,只有将数字值与上述特定的测量方法相关联,这些数字才能表达物理量的数字值。
基本物理量的数字值与所选择的单位有关,而物理量是独立存在的,与所选择的单位没有关系。我们的食指长度总是相同的,与我们用厘米作为单位或是用英尺作为单位测量是没有关系的。一个物理量可以用单位a测量,也可以用单位a’测量,但物理量在物理上是相同的,也即
A=Aa={A}'{a}'
如果{a}'= na,那么就有{A}'= n^{-1}A。
这表明如果基本物理量的单位尺寸变化n倍,那么所得的测量结果就会变成n-1倍。
按惯例,总是用同一单位测量同一种物理量,因此当物理量的单位大小发生变化时,所有的基本物理量也会发生同样比例的变化。也就是说,同种物理量的任意两种物理量的数字值之比是与基本单位无关的。
值得注意的是,同种基本物理量在物理上相加时(A+B=C)时,数字值也满足同样的方程(A+B=C)而不必考虑所用的测量单位。换句话说,数字方程是模仿物理方程的,并且它们的形式与单位大小无关。
2.4导出数量、量纲以及无量纲数量
在定量描述物理事物和事件时,我们会引用基本数量的数字值,同时将这些数字值插入相应的数学方程时还会引入更多的数字值。比如,通过测量物体运动的距离和时间来计算速度V=lt-1,或者我们测量物体的质量和运动速度来计算它的动量k=mV2/2。这些数字就是第一种类的导出物理量。
将基本物理量插入数学方程中所得到的数字并非都是物理量6。基本物理量有一个明确的物理含义,基本物理量的两个样品的比例不会因为基本单位大小的改变而改变;任意选择的单位不会影响物理量的数量。Bridgman(1931)认为事实上这定义了所有物理量的特性(attribute)。这也就是Bridgman的相对数量值的绝对意义原理:
将基本物理量插入数字方程年得到数量Q,如果它的基本单位改变后,
两个样品之间的比例不发生变化,那么数量Q就是物理量。
Bridgman继续阐述了指数方程符合相对数字绝对意义的概念(Bridgman,1931;Barenblatt在1996年也证明了这个问题):
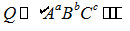
其中A、B、C等等是基本物理量的数字值,而系数α及指数a、b、c等等都是实例,它的值可以用来区分一种导出数量与另一种导出数量。所有的单项式导出数量都是指数形式的,其它形式都不能代表物理量。
我按照数字值的概念定义第一种类导出物理量,第一种类导出物理量同基本单位的选择相关,它不必同基本物理量那样能表达明确的事物,当然它也可以表达明确的事物。比如,时间的平方要是导出物理量,因为它是满足指数规则的,但是我们却不能明确地指出时间的平方根“就是”某一种物理事物。
没有物理实体的物理量的数值与基本单位相关,为了避免谈及这样的物理量的单位,我们引入量纲的概念。每一种类型的基本物理都是按它自身的量纲来定义的。如果A长度的数字值,我们就说它有长度量纲,并且写着[A]=L,这里,方括号表示量纲,而L将长度概念符号化了。通过这个方法,我们可以简单地表示:如果长度单位的大小变化了n倍,那么数字值将会变化n-1倍。
导出物理量的量纲以同样的方式传达了从基本物理量导出的信息。设想按方程定义的物理量为:

其中L_{i}^{i}是一定长度的数字值,M{i}^{m_{}i}是一定质量的数字值,而t{i}^{i}是一定时间的数字值,所有的指数都是实数。如果长度单位变化为nL倍,质量单位变化了n_{m}倍并且时间单位变化了n_{t}倍,那么按照上述方程,数量Q将会变化n^{-1}:

其中:
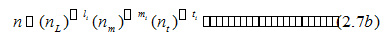
这表明数量Q的变换与基本数量的变换一样,它的单位是n\square L^{\square l_{i}}M^{\square m_{i}}t^{\square t_{i}}有比例关系,而L、M和t分别是长度、质量和时间基本数量的单位。量纲也有类似的推理过程,因此我们可以说导出物理量量纲是:
无论是应用到基本物理量还是导出物理量,量纲都简单地表达了当基本物理量的单位发生变化时,它的数字值应该如何发生变化。导出物理量的量纲满足它的定义方程式。为了获得按(2.6)式定义的物理量的(2.8)式的结果,我们只需要简单用量纲符号替换(2.6)中的基本物理量,忽略数字系数α,就能从代数上获得(2.8)式。比如,动能\left ( mV^{2}/2 \right )的量纲是M(L/t)^{2}\square ML^{2}t^{\square 2}。
物理量的量纲是“表达它的基本特性”(Tolman,1971)这样的话是对于基本物理量来说是毫无意义的同意反复,而对于导出物理量来说,也是废话。我们应该看到,物理量的量纲与单位系统的选择有关,并且因此也受观察的影响,它不是物理量的本质属性。
按照习惯,特定的导出物理量的表达式是数字值加上它的单位组成,导出物理量的单位由基本物理量单位组成,组成形式同导出物理量的量纲是一致的。Q=0.021kgs1/2表明Q是一个物理量,它的量纲是Mt1/2,如果质量是用kilogram单位测量而时间是以秒来测量,那么它的数量值是0.021,简言之,可以说:物理量Q是以单位kgs1/2来测量的,它暗示了物理量的量纲及所使用的基本单位。按照通俗的说法,单位和量纲这两个术语同义语,但在专业著作中,不希望采用这种说法,因为在专业著作中,明确基本概念是最主要的问题。
关于导出物理量有以下几点值得我们注意:
- 导出物理量的量纲都是基本物理量量纲的幂积。
- 同量纲的导出物理量的和的量纲与导出物理量量纲相同。
- 当基本单位发生变化时,同量纲的所有导出物理量都会改变它们的值,改变的比率与基本单位改变比率相同。
- 如果导出物理量的数字值保持不变,那它导出物理量是无量纲的。比如,导出物理量Vt/L,V=dx/dt是速率,t是时间并且L是长度。无量纲物理量是具有单一性(unity)的特性,它只是一个比例因子,随着基本物理量的单位大小发生变化而变化。
- 通常情况下,有量纲的导出物理量在特殊函数(对数、指数、三角函数等等)作用下得到的导出量不是导出物理量,原因在当基本物理量的单位大小发生变化时,这些函数的导出量不能满足卖出物理量的要求。只有这些特殊函数的参数是无量纲物理量时,这时在基本物理量的单位变化时,这些函数的值保持不变。因此当用无量纲的物理量作特殊函数的函数值才是导出物理量,这个导出物理量也具有量纲单一性的特点。
2.5物理方程、量纲齐次性和物理常数
在对物理事件做定量分析时,人们要搜寻描述这些事件物理量之间的数学关系。然而,我们不会对物理量之间的所有关系都感兴趣。原始人发现在数字上他自己的以kg为单位身体质量会精确地与他自己的以inche为单位的身高相等,并且会认为这是不可思议的,甚至还可能会认为这是一种奇迹。但我们会发现这其实只是我们选择单位进行测量后偶然所得的结果。科学家仅仅只关心那些能表达一个物理量与多个物理量之间的物理关系,即他们只关心是物理方程。对于我们随意所选择的测量单位来说,自然特性还是那样的自然特性,没有差别。因此,我们只会关心那么与测量单位无关的数字关系。
这也就会对可能的物理方程产生一定的约束。假设对于一个特定的物理事件,物理量的数值Q0由其它物理量的数值Q1...Qn决定,即
Q_{0}= f\left ( Q_{1},Q_{2}, \cdots ,Q_{n}\right )\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \left ( 2.9 \right )
绝对意义相对值原理告诉我们式(2.9)告诉我们如果当任何一个基本单位变化时,Q0,也即f按相同的比例发生变化,那么就这个方程式在物理上是相关的。换句话说,物理方程必须在量纲上是齐次的(homogeneous)。在本节结尾处针对量纲齐次性所做的深入讨论和总结会提示出量纲齐次性会强制要求如同式(2.9)的方程式满足以下的约束条件:
- 方程两边的量纲必须是相同的;
- 无论物理量在方程中如何相加,所有相加的项的量纲必须是相同的
- 方程中的指数函数、对数函数、三角函数等等特殊函数的参数必须是无量纲的。
比如,物理方程如下:
A= Be^{c}-\frac{\left ( D_{1}+D_{2} \right )}{E}+F\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots\left ( 2.10 \right )
那么C就必须是无量纲的,D1和D2必须是同量纲的,而A、B、D/E和F必须有相同的量纲。
量纲齐次性的一个结果就是物理方程的形式与单位大小是无关的。下面的初值也可能对于解决为什么要求物理方程具有量纲齐次性有帮助,并且能提示出如果不能保证齐次性会如何引起概念上的错误。假设我们在均匀的重力场中,比如真空中,让一个物体下落,并且问在时间t时它会下落多少距离x。我们当然知道基本牛顿力学原理,它给出的答案是:
x= \frac{1}{2}gt^{2}\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \left ( 2.11 \right )
其中g是当时的重力加速度,它有Lt-2的量纲。这一物理方程表达到物理规律,很清楚,它是量纲齐次的。
当我们从不能视角来审视同一物理现象时,量纲齐次性是显而易见的。假设我们还不知道力学原理,并且在剑桥大学、曼彻斯特大学进行大量的关于真空中质量为m的物体在时间t内下落的距离x的试验。当进行了各种各样的质量和距离的试验后,我们会发现如果用秒作测量单位测量时间t、以米为单位测量距离x,所有的数据都会与方程相吻和,而且这个方程与物体质量无关:
x= 4.91t^{2}\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots\cdots \left ( 2.12\right )
这个方程是完全正确的。它精确地描述和预测了所有(在剑桥大学和曼彻斯特大学)的试验。然后,然而初初一看,这个方程似乎是量纲非齐次的,在方程两边似乎有不同的量纲,方程也似乎不似物理方程。然而,这种印象来源于一个错误的推定,即系数4.91在测量单位发生变化时它是不变的。事实上,系数4.91并非是无量纲的数,它是一个有量纲的物理量的数字值,它体现了剑桥地区x和t之间的关系,这一点很清楚了,即当测量单位发生变化时,我们必须考虑应该如何转换方程(2.12)。我们知道,当变换测量单位时,真实的物理量x是不会发生变化的,因此如果我们下落距离用英尺来测量,方程(2.12)的右边应该乘以3.28,这个数表示一米有3.28英尺。因此,如果x用英尺来测量,t用秒来测量,那么方程(2.12)的正确版本就应该是:
x=16.1t^{2}\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots\cdots \left ( 2.13\right )
因为方程(2.12)是表达了普遍性的物理规律,因它按照Bridgman的绝对意义相对值的概念,它应该是量纲齐次的,所以上述变换应该还有很多方式,因此,方程的正确书写格式应该是:
x= ct^{2}\left ( c= 4.91ms^{-2} \right )\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \left ( 2.14\right )
这种格式就非常清楚,这表明了系数是物理量而非数字值。c的单位指明了它的量纲并且提示了长度单位由米变换成英尺且时间单位保持不变时,c变化比例因子是3.28,这是长度单位变化因子的逆。这样,c=16.1fts-2,如同方程(2.13)所示。
方程(2.14)的格式可以正确地表达方程(2.11)的数据概念。它是量纲齐次的,并且在基本单位化后,利用它来做变换更易使人明白。
每一个正确的物理方程,也即能正确表达物理量的数字值之间的关系的每一个方程都必须是量纲齐次的。从正确的原始数据所得的适当方程式初初一看可能是量纲非齐次的,这可能是因为选择了特定的基本单位进行测量的缘故。一般地,这样的公式可以按以下几个步骤将它改写成量纲齐次的(Bridgman,1931):
- 用未知量纲的常数取代方程中的所有数字系数;
- 要求新的方程是量纲齐次的,由此推定这些常数的量纲;
- 当使用单位相同时,将这些常数与原方程相对应,从而确定这些常数的数值;
毫无疑问,方程(2.14)就是按方程(2.12)经过这三个步骤导出的。
我们可以再用一个实例来加深印象。假设在美国上方大气层的压力分布可以用下述方程描述:
p= 1.01\times 10^{5}e^{-0.00012z}\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \left ( 2.15 \right )
其中,p是以单位Nm-2为单位的压力值,而z是以米为单位的高度值。这个表达式仅对使用的单位是合适的。正确的、量纲齐次的方程应该是以下的格式:
p= ae^{-bz}\left ( a= 1.10\times 10^{5}Nm^{5},b= 0.00012m^{-1}\right )\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \left ( 2.16 \right )
其中a和b是物理量。这一格式的方程是与选择的单位无关的。a和b的量纲表明了当基本单位变化时,这些物理量的数值会发生什么样的变化。
方程(2.16)中的a和b两个物理量是物理常数,一旦选定了单位系统它们的值就固定下来了。从这个方面来看,这两个常数特征化了特定环境下,即美国上空的大气压力分布规律。类似地,在方程(2.11)中的重力加速度也是一个物理常数,它特征化了(当地!)地球表面的重力场。
物理学规律中还包括了大量的宇宙常数,一旦选择了单位系统,它们的数字值也同这两个实例一样是固定的,比如:真空中的光速c,宇宙引力常数G,Planck常数h,波尔兹曼常数kB等等。
2.6第二种导出物理量
按照基本物理量和导出物理量来划分物理量还不全面。还有一些通用规律,它们按一定的关系将不同种类的物理量组合到一起,并且这些规律可以用来将基本物理量转换成导出物理量。由于降低了必须随意选择的单位数量,简化了这些物理规律的表达形式,因此这些转换是必要的。
比如:面积按照它的比较操作和加法操作的定义,是可以视为基本物理数量的,我们可以随意地选择一个单位来测量它:比较荒唐的想法是用一张邮票作为测量单位。室内的地面面积就可以用这种邮票或者邮票的一部分来覆盖,并且我们可以记录总计所用的邮票数量。如果我们这样测量,不考虑我们选择的测量单位来测量面积A,最终我们会发现,按照方程(2.17),它的数字值A依赖于它的线性尺寸:
A=c\int dxdy\cdots \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\left ( 2.17 \right )
这里的积分是在整个面积上的积分,c是一个有量纲的常数,它的数字值依赖于所选择的面积和长度的基本单位。量纲齐次性要求常数c是一个量纲为AL-2的导出物理量:
c=\frac{A}{\int dxdy}\cdots \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\left ( 2.18 \right )
方程(2.17)也可以视作“物理规律”。然而,我们稍稍思考一下就会发现,这个方程不具有简单性,虽然我们已符号化为dxdy的物理量是按照比较操作和加法操作规则来定义的,不过它是碰巧与我们为面积定义的比较操作和加法操作相似的,因此方程(2.17)不是真正的自然规律,它不过是某一个人为我们做的一个手工艺品而已。
像方程(2.17)中的有量纲的常数c,它的数字值依赖于我们所选择的测量单位,但整个来看,它又与我们所考虑的问题无关,因此我们称他们为宇宙常数。
方程(2.17)是可以简化的。如果我们选择用一种单位来测量面积,而这种单位是一个正方形的面积,它的边长是长度单位,那么物理常数c就是1(unity),并且方程(2.17)就变成了:
A=\int dxdy\cdots \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\left ( 2.19 \right )
从效果上看,面积就变成了导出物理量,它是按照涉及长度的操作来定义的。现在,从物理上来看,方程(2.19)并没有暗示面积“是”长度的平方。面积仍然保留了原来的物理特性,很容易与长度区分开来,但是也同长度的平方区分开来了,长度的平方无论如何是没有任何物理意义的概念。我们已注意到,事实上“积分”的概念和“面积”的概念是相似的,我们可以选择通过涉及长度的操作来测量面积,事实上我们也是这样决策的。现在事实就是面积有L2的量纲,这表面这样定义的面积在长度单位变化n倍时,面积单位会以n-2倍变化。
用这种办法将面积这一基本物理量转换成了导出物理量,我们完成了两个简化:长度单位自动地确定了面积单位以及用1(unity)代替了方程(2.17)中的有量纲物理常数c。
选择c=1做转换没有任何损失。如果我们采用直径为一个长度单位的圆为面积单位,那么面积的定义就是A=\left ( \frac{4}{\pi } \right )\int dxdy而不是方程(2.19)。这个方程也是非常完美的,但是因为它迫使我们要浪费大量的纸张来书写意义不大的4/\pi ,所以它同我们日常所用的惯用方法不合。在其它情况下,引入不是1(unity)的无量纲系数,应用起来更为方便。比如,定义动能为K= mV^{2}/2而不是K= mV^{2},可以使得在引力场中质点的能量方程可以读作K+U=常数,而不必读成K/2+U=常数,其中U是势能。类似地,将4\pi 放到Gauss和Amper定律的积分形式中就是为了消除其微分形式(Maxwell电磁场方程)中的数字系数。
速度是另外一个类似于面积的实例。我们是可以定义速度是一个基本物理量的,因为它有自己的比较操作和加法操作,并且可以为它选定一个基本单位,比如,我们再一次用一个比较荒谬的想法,我们选定一个非常稳定的、吹向水平面上的一个儿童玩具的风的速度为速度的基本单位。如果我们这样处理这个问题,最终我们会发现,事实上速度物理量是与单位时间内的距离成正比的。那么我们可以选择定义速度是一个导出物理量V=dx/dt,这样就会等效于我们选择在单位时间内的距离作为速度单位。
更为有趣的实例就是力。力可以作为基本物理量,可以选择任意特定的单位—比如拉伸标准弹簧至一个标准长度时的力。Newton定律最开始时是这样陈述的:在非相对论条件下,如果一个物体(更准确地说应该是一个质点),其质量为m,它受到的合力为F(比如在x方向上),它会在合力方向加速,它的加速度a=d^{2}x/d^{2}y是与力F和质量相关的,它可以写成:
F=cma\cdots \cdots\cdots\cdots\cdots\cdots\cdots\cdots \cdots\cdots\cdots\cdots\cdots\cdots\left ( 2.20 \right )
其中,系数c是宇宙常数,如果力、长度、质量和时间都选择为基本物理量,它的量纲是Ft2M-1L-1。方程(2.20)就是通常用来描述质点动力学中三个不同物理量,即力、(引力质量)和加速度之间的数值关系的方程。
然而我们可以自由地选择力的单位,比如我们选择在非相对论条件下,给定单位质量和单位加速度时的力为力的单位。如果这样,我们就能使得方程(2.20)中的常数c=1,并且将Newton定律写成没有常数的形式:
F=ma\cdots \cdots\cdots\cdots\cdots\cdots\cdots\cdots \cdots\cdots\cdots\cdots\cdots\cdots\left ( 2.21 \right )
其中力的量纲是MLt-2。方程(2.21)在物理意义上并不表示力“是”质量乘加速度,事实上在物理上根本没有定义质量与加速度的积,并且在任何情况下,没有质量和加速度的情况下力也是存在的,比如当用力推砖墙(砖墙不动,并且给我等值相反的力)时。与面积和速度的实例相反,方程(2.21)并没有提供在任何情况下,在通过在现场作基本物理量的测定的方法,来直接计算力的可能性。相反,依据质量和长度单位这一特定方式,赋予了力导出物理量的特性。
通过选择单位有目的地应用普通物理规律来将物理量转化为导出物理量,那么这样的导出物理量我们称之为第二种类导出物理量。力是一个实例,在SI单位系统中,热能和电荷也是这样处理的。
2.7单位系统
单位系统定义为:
- 具有比较操作和加法操作的基本物理量的完整集合。
- 基本单位
- 所有导出物理量。如果它们是第一种类的导出物理量,要列出它们的定义方程(比如V=dx/dy),如果它们是第二种类的导出物理量,则要列出定义它们单位的物理方程(比如在SI单位系统中定义力的单位的方程F=ma)。
导出物理量是一个开放集,在分析中可以随人的意愿加入新的导出物理量。
单位系统也同样是开放集,只是在基本单位的数量值方面,它与导出物理量有差别。
在SI (Système International)单位系统中有七个基本物理量(表2.1),它们分别是:长度、时间、质量、温度、电流强度、基本粒子数以及发光强度(luminous intensity)。长度、时间和质量单位分别是米(m)、秒(s)和千克(kg)。按Newton力学定律F=ma,力被定义为导出物理量。
在任何单位系统中,温度都必须是热力学温度。用任何一种方法制造的温度计都可以读出温度的度数,并且还可以在两个温度量之间进行比较,但是物理量并非数字值(2^{\circ}C会是1^{\circ}C两倍那么热吗?0^{\circ}C就是温度为“零”,表示没有温度吗?如果将温度定义为任意制造的温度计上的一个刻度值,那么如果解释热从高温向低温流动呢?)然而,热力学温度(或者称为绝对温度)是按物理的比较操作和加法操作来定义的,它是一人基本物理量。通过Carnot机可以测量出两个绝对温度的比值,温度的单位(比如“度”的大小)是可以任意选择的。SI中温度的单位是开尔文(kelvin)(K),它的大小是水三相点温度的1/273.16。
表2.1 SI单位系统
基本单位
| 物理量 | SI单位名 | SI符号 |
| Length L | meter | M |
| time t | second | s |
| mass M | kilogram | kg |
| temperature T | kelvin | K |
| current I | ampere | A |
| number of elementary particle | mole | mol |
| luminous intensity | candela | cd |
导出物理量(不完全)
| 物理量 | 定义方程/规律 | 量纲 | 量纲符号 | 名称 |
| area | A=\int dxdy | L^{2} | m^{2} | --- |
| volume | V=\int dxdydz | V=m^{3} | m^{3} | --- |
| frequency | f=1/ \tau | t^{-1} | s^{-1} | hertz\left ( Hz \right ) |
| velocity | V=\frac{dx}{dt} | Lt^{-1} | ms^{-1} | --- |
| acceleration | a=\frac{d^{2}x}{d^{2}t} | Lt^{-2} | ms^{-2} | --- |
| density | \rho =\frac{F}{V} | ML^{-3} | kgm^{-3} | --- |
| force | F =ma | MLt^{-2} | kgms^{-2} | newton(N) |
| stress/pressure | P =F/A | L^{-1}t^{-2} | Nm^{-2} =kgm^{-1}s^{-2} | pascal(Pa) |
| work/energy | W =\int Fdx | L^{2}t^{-2} | Nm =kgm^{2}s^{-2} | joule(J) |
| torque | T =Fl | ML^{2}t^{-2} | Nm =kgm^{2}s^{-2} | --- |
| power | dW/dt | ML^{2}t^{-3} | Js^{-1} =kgm^{2}s^{-3} | watt(W) |
| charge | Q=\int ldt | It | As | coulomb© |
在SI单位系统中,电流强度被选作基本物理量而电量却被选作了导出物理量(通过Q=\int ldt)。电流强度的单位是ampere(A)。电流强度的单位A按如下方法定义:在真空中相距一米的两个无限长的平等导体之间、在每单位长度上产生的力为 2\times 10^{-7}N时,导体中的电流强度就是1A。转换因子 2\times 10^{-7}是为了转换的需要,也有其历史原因,它出现在了SI版本中的Ampere定律中。
mole单位保留在SI单位系统中作为特定的物质的量:它不是对物质的一个一个的记数,而是对Avagadro数(6.02×1023)的记数。但是在使用这个单位时,必须要指明记数的基本物质是什么,比如应该使用“1mole原子、1mole分子、1mole网球”等等。值得注意的是SI的mole单位实际上就是老的“克摩尔”单位。
照明强度(luminous intensity)不是指每单位空间角的全部辐射能量(瓦特每球面度),是指“人眼”最敏感的那一部分辐射能(定义为标准响应曲线)。人眼对波长为555纳米的光最敏感,因此1cd就等效于1.46\times 10^{-3}瓦特每球面度。
在基本物理量中还包括两个无量纲的平面角和球面角,分别用弧度和球面度测量。我们认为它们是导出物理量固然是因为它们是无量纲的量,但更重要的是它们的定义涉及到对长度的操作,这一点更像对长度的操作来定义面积。
我们再一次注意到导出物理量的量纲与所选择的单位系统有关,而单位系统控制观察的过程有关,并且对于物理量的本质特性没有任何影响。肯定地,物理量是有一定的物理含义的,比如功和力矩有相同的量纲,但它们却是本质不同的两个物理量。
单位系统对物理量的量纲的影响可见表2.2,表中显示了三种不同单位系统下某些力学量的量纲。如果基本单位各类相同但数值不同,那么单位系统也会是相同的类型,而且导出物理量和基本物理方程都有相同的数学形式,仅仅是方程中的物理常数不一样。
在表2.2中第一个系统类型将长度、时间和质量作为基本物理量,力的单位通过质量和加速度以Newtom定律F=ma来定义。SI单位系统和cgs(厘米、克和秒)单位系统都这种系统类型。在第二个系统中,长度、时间和力是基本物理量,而质量也是通过F=ma来定义的。大不列颠重力系统(British Gravitational System)就是这样的实例,在这个系统中,基本单位是英尺、秒和磅力(lbf)。1lbf的力就是标准质量标本上的标准重力(32.2ft/s2),这里标准质量标本的质量是1磅质量(因此也就换为“重力系统”)。在这个系统中,质量是导出物理量,它的量纲是Ft2L-1,单位(“slug”)就是磅质量,等于32.2克。在第三个系统中,长度、时间、质量和力都被选择为基本物理量,而Newton定律写成F=cma,其中c是物理常数,具有Ft2M-1L-2的量纲。不列颠工程系统(British Engineering System)是它的实例。在这个系统中,基本单位是英尺、秒、磅质量和磅力,而Newton定律的物理常数是c=1/32.2lbfs2lbm-1ft-1。
表2.2不同单位系统中某些力学量的量纲
三种单位系统类型中的基本单位和量纲
| Type1 | Type2 | Type3 | |
| 基本物理量和量纲 | L,M,t | L,F,t | L,M,F,t |
某些导出物理量的量纲
| velocity=dx/dt | Lt^{-1} | Lt^{-1} | Lt^{-1} |
| Acceleration=d2x/dt2 | Lt^{-2} | Lt^{-2} | Lt^{-2} |
| mass | M | Ft^{2}L^{-2} | M |
| area=\int dxdy | L^{2} | L^{2} | L^{2} |
| Force |
| c=F/ma Newton'定律 | c=1 | c=1 | FM^{-1}L^{-1}t^{2} |
| Work=\int Fdx | ML^{2}t^{-2} | FL | FL |
| stress=F/A | ML^{-1}t^{-2} | FL^{-2} | FL^{-2} |
表2.2提示了这样一个事实,即当真实的物理量,比如力无论任意选择什么单位系统它是相同的。但它的量纲却依赖于单位系统的选择。依赖于如何定义导出物理量,给定的物理定律方程中可能会包含有量纲的物理常数,我们必须依据所选择的单位系统来确定这个物理常数值(比如在F=cma中),也可能这个常数值是1(仍然是由单位系统所确定的)。
值得注意的一个有趣现象就是仅有少量的几个物理定律用来将基本物理量转换为导出第二种物理量。还有大量的定律保持了有量纲的物理常数,从概念上,这些常数是可以设置为1(unity)的:比如引力常数G、Planck常数h、波尔兹曼常数kB、真空中的光速等等都可以被设置为1(unity)。这让我们可能做一些有趣的事。比如,我们可能定义一个单位系统,它没有基本单位(Bridgman,1931)。在这个系统中,所有的测量单位都与描述我们的宇宙的宇宙常数相关,其效果就是的确存基于宇宙常数,比如光速、量子能等等常数的,有关基本物理量的宇宙“自然”单位。不幸的是,选择这样的“自然”单位系统不但没有良好的使用性能,反而会使得我们努力希望赋予这些单位良好特性的努力付诸东流。
2.8总结
- 基本物理量是可以定义物理操作的属性:这些物理操作就是比较操作和加法操作。比较操作是确定物理量的两个样品值相等与否的过程,而加法操作是属性的两个样品值相加后的含义的过程。
- 基本物理量是一种物理属性,针对这个物理属性可以定义物理操作:加法、减法以及与纯粹数字之间的乘法和除法。没有为物理量定义的物理操作是乘积、比例、幂以以及对数函数、指数函数、三角函数和其它特殊函数。
- 基本物理量可以任意选择它自己测量单位进行测量并得到相应的数字值。
- 第一种类导出物理量是基本物理量的各种各样的幂积。导出物理量由(依赖于基本单位的大小)的数字来定义,并且不必有明确的物理表达形式。
- 物理量的量纲,无论它是基本单位还是导出单位,它都表达了当基本单位变化时导出物理量的数字值的变化方式。物理量量纲不能提供物理量的本质特性。同一个物理量(比如力)在不同的单位系统中可以用不同的量纲,而且具有明显不同的物理意义的物理量可能会有相同的量纲(比如功和力矩)。
- 物理量之间的关系可以用这些物理量之间的数字值关系来表达。正确描述物理量之间关系的数学方程应该是量纲齐次的(见2.5),无论基本单位如何变化也能使这样的方程保持有效。
- 物理量的分类,无论是基本物理量还是导出物理量都有一定程度的随意性。如果一特定的物理量某一特定的物理量被证明是通过某一宇宙定律与某些其它的基本物理量相关,如果我们愿意,就可以应用这个定律来重新将这个物理量定义为第二种类导出物理量,并且它的数字值依赖于其它单位的选择。所有的基本物理量按这种方式转换成了第二种类导出物理量后,仍然保持它自身所有的物理特性(比如:它的比较操作和加法操作特性)。通过第二种类的导出物理量的定义方程由其余的基本物理量可以直接确定它的数字值,也可以从其余的基本单位导出它的单位来间接确定。
- 单位系统由(a)基本物理量、(b)基本物理量的单位及(c)导出物理量,包括导出物理的定义方程或者是将基本物理量转换成导出物理量的方程一同构成。基本物理量的类型和数量是可以任意选择的。
5Sir Arthur Eddinton(1939):“时间作为一种新的物理量为人们的实践所接受。它应该被认为是一系列测量和计算的结果。人们根据这些结果形成心理上的图形,从而在形而上学的王国里达到自娱自乐的目的,那是风险自负的,物理不会为此负责。”
6从这一点来看,术语数量只是指物理量的数字值,否则另有所指才会有其它含义。
7比如:两个物理热力学温度的数字值之比T1和T2之比被定义为Carnot机的热效率h12。Carnot机是在两个温度不同温度的蓄热器之间操作热流的机器。如果T1是是热量流入的蓄热器温度,那么T_{1}/T_{2}=1-\eta _{12},其中\eta _{12}是一个纯粹的数字。这样为两个温度T1和T2这间的数字比值提供了物理操作,并且暗示了一个物理量的物理加法操作:如果T_{1}=nT_{2},其中n=T_{2}/T_{1},那么T_{1}+T_{2}\equiv T_{3}=\left ( 1+n \right )T_{1}。如果Carnot机运行在温度T_{3}和温度T_{1}之间,那么可以用物理概念可以识别出温度T_{3}=\left (1+ n \right )T_{1},它表示此时Carnot机的热效率为n/(1+n)。
编者按:
《量纲分析物理基础》是中铁五局陈跃龙先生生前译著,陈跃龙先生是卓越的混凝土专家,专业领域之外,他涉猎甚广,尤其对于物理领域更是有独特的见解。《量纲分析物理基础》是陈跃龙先生十分推崇的著作,量纲分析为我们提供了简化物理问题的方法,从而能获得对物理问题的定量解答,该作品更是以通俗化的角度来解释物理量传递的规则,强调物理量之间的逻辑关系,有助于广大读者去理解。对于理工科的土木工程人,增加对物理量纲的理解,更有助于我们去理解或解释土木工程基础技术。

十分感谢您阅读我们网站的文章。如需转载原创文章,敬请注明文章出处及作者,并设置跳转到原文的链接!